Berapa jarak dari pusat ke keliling lingkaran? Cari tahu di sini! Mungkin Anda pernah belajar tentang lingkaran di sekolah dulu, tetapi apakah Anda tahu betapa menariknya menggali lebih dalam tentang konsep ini? Bagaimana jarak dari pusat lingkaran ke titik-titik di sekitarnya dapat memainkan peran penting dalam perhitungan geometri. Mari kita bersama-sama mendalami konsep ini dan mengeksplorasi lebih lanjut mengenai jarak yang menarik ini. Yuk, sambut petualangan baru kita dengan membaca artikel ini hingga tuntas!
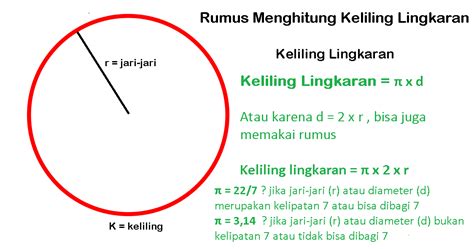
Jarak Dari Pusat Ke Keliling Lingkaran
Penjelasan tentang jarak dari pusat ke keliling lingkaran, yang juga dikenal sebagai jari-jari lingkaran, sangatlah penting dalam studi matematika mengenai lingkaran. Jarak ini mengacu pada jarak antara titik pusat lingkaran dengan titik-titik pada keliling lingkaran. Mengetahui jarak ini akan membantu kita memahami sifat-sifat dan rumus-rumus matematika yang berkaitan dengan lingkaran.
Pengertian Jarak Dari Pusat Ke Keliling Lingkaran
Jarak dari pusat ke keliling lingkaran, atau yang sering disebut sebagai jari-jari lingkaran, adalah jarak antara titik pusat lingkaran dan titik-titik pada keliling lingkaran. Jarak ini bisa diukur menggunakan satuan panjang seperti centimeter, meter, atau yard. Dalam matematika, jarak ini memiliki peran penting dalam mempelajari sifat-sifat dan rumus-rumus yang berkaitan dengan lingkaran.
Rumus Jarak Dari Pusat Ke Keliling Lingkaran
Ada beberapa rumus yang dapat digunakan untuk menghitung jarak dari pusat ke keliling lingkaran, tergantung pada informasi yang kita miliki mengenai lingkaran tersebut. Beberapa rumus yang sering digunakan adalah:
– Untuk mencari jari-jari lingkaran jika diketahui keliling, kita dapat menggunakan rumus jari-jari (r) sama dengan keliling (K) dibagi dua kali π. Rumusnya adalah r = K / (2π). Rumus ini sangat berguna saat kita memiliki informasi mengenai keliling dan ingin mencari jari-jari lingkaran.
– Untuk mencari jari-jari lingkaran jika diketahui luas, kita dapat menggunakan rumus jari-jari (r) sama dengan akar kuadrat dari luas (L) dibagi π. Rumusnya adalah r = √(L / π). Rumus ini berguna ketika kita memiliki informasi mengenai luas dan ingin mencari jari-jari lingkaran.
– Untuk mencari luas lingkaran jika diketahui jari-jari, kita dapat menggunakan rumus luas (L) sama dengan π dikalikan r kuadrat. Rumusnya adalah L = πr^2. Rumus ini berguna ketika kita memiliki informasi mengenai jari-jari dan ingin mencari luas lingkaran.
Penerapan Jarak Dari Pusat Ke Keliling Lingkaran
Pengetahuan mengenai jarak dari pusat ke keliling lingkaran memiliki berbagai penerapan dalam berbagai bidang studi dan aplikasi matematika. Beberapa contoh penerapannya adalah sebagai berikut:
– Dalam bidang geometri, jarak dari pusat ke keliling lingkaran digunakan untuk menghitung panjang busur lingkaran. Panjang busur lingkaran dapat dihitung dengan rumus panjang busur (s) sama dengan sudut pusat (θ) dikalikan jari-jari (r) atau s = θr. Selain itu, jarak ini juga penting dalam menghitung luas lingkaran dengan menggunakan rumus luas (L) sama dengan π dikalikan r kuadrat.
– Dalam bidang fisika, jarak dari pusat ke keliling lingkaran dapat digunakan untuk menghitung momen inersia suatu lingkaran. Momen inersia adalah ukuran kecenderungan suatu objek untuk tetap diam atau tetap bergerak setelah diberikan gaya. Momen inersia sebuah lingkaran dapat dihitung dengan rumus momen inersia (I) sama dengan setengah kali massa (m) dikalikan jari-jarinya kuadrat atau I = 1/2mr^2. Jarak dari pusat ke keliling lingkaran menjadi faktor penting dalam perhitungan ini.
– Dalam dunia teknik, jarak dari pusat ke keliling lingkaran sangatlah penting dalam membangun struktur bangunan dan merancang objek-objek berbentuk lingkaran seperti roda gigi, roda mobil, atau roda layang-layang. Pengetahuan tentang jarak ini memungkinkan perancang untuk menghitung dengan tepat ukuran dan posisi pusat lingkaran pada objek yang akan dibuat.
Dengan demikian, dapat kita simpulkan bahwa pengetahuan tentang jarak dari pusat ke keliling lingkaran memiliki peran yang sangat penting dalam berbagai aspek matematika dan penerapannya dalam dunia nyata. Dengan menggunakan rumus-rumus yang tepat, kita dapat menghitung berbagai parameter dan sifat-sifat lingkaran yang akan memudahkan kita dalam memecahkan berbagai masalah matematika dan teknik.
Gambarkan pola lantai diagonal memainkan peran penting dalam pembangunan dan desain lantai.
Sifat-sifat Jarak Dari Pusat Ke Keliling Lingkaran
Sifat pertama dari jarak dari pusat ke keliling lingkaran adalah bahwa jarak ini sama untuk semua titik pada keliling lingkaran. Ini berarti bahwa jika Anda mengukur jarak dari pusat lingkaran ke titik mana pun pada keliling, hasilnya akan selalu sama.
Sifat kedua dari jarak dari pusat ke keliling lingkaran adalah bahwa jarak ini mencapai nilai terbesar pada keliling lingkaran. Ini berarti bahwa setiap titik pada keliling lingkaran memiliki jarak yang sama dengan jarak terbesar dari pusat lingkaran.
Sifat ketiga dari jarak dari pusat ke keliling lingkaran adalah bahwa jika jaraknya berubah, keliling lingkaran juga akan berubah. Jarak yang lebih besar akan menghasilkan keliling yang lebih besar, sedangkan jarak yang lebih kecil akan menghasilkan keliling yang lebih kecil.
Ketika kita membahas tentang jarak dari pusat ke keliling lingkaran, ada beberapa sifat penting yang perlu kita ketahui. Sifat-sifat ini membantu kita memahami hubungan antara jarak dari pusat ke keliling dan karakteristik lain dari lingkaran. Dalam artikel ini, kita akan menjelaskan secara detail tiga sifat penting dari jarak dari pusat ke keliling lingkaran.
Sifat Pertama: Jarak Dari Pusat Ke Keliling Sama Untuk Semua Titik
Sifat pertama dari jarak dari pusat ke keliling lingkaran adalah bahwa jarak ini sama untuk semua titik pada keliling lingkaran. Ini berarti bahwa jika Anda mengukur jarak dari pusat lingkaran ke titik mana pun pada keliling, hasilnya akan selalu sama.
Jarak dari pusat ke keliling lingkaran ini dikenal sebagai radius. Radius adalah jarak terpendek antara pusat lingkaran dan titik pada keliling. Baik titik mana pun yang Anda pilih pada keliling, jaraknya akan selalu sama dengan panjang radius.
Hal ini dapat diilustrasikan dengan melakukan percobaan sederhana. Anda dapat mengambil seutas tali dan mengikatkannya pada pusat lingkaran. Kemudian, tarik tali ke arah titik mana pun pada keliling dan ukur panjang tali tersebut. Anda akan menemukan bahwa panjang tali tersebut sama dengan panjang radius lingkaran.
Misalkan Anda memiliki lingkaran dengan radius 5 cm. Jika Anda mengukur jarak dari pusat ke keliling pada titik mana pun pada keliling, hasilnya akan selalu 5 cm.
Sifat Kedua: Jarak Terbesar pada Lingkaran
Sifat kedua dari jarak dari pusat ke keliling lingkaran adalah bahwa jarak ini mencapai nilai terbesar pada keliling lingkaran. Ini berarti bahwa setiap titik pada keliling lingkaran memiliki jarak yang sama dengan jarak terbesar dari pusat lingkaran.
Untuk memahami sifat ini, perlu diketahui bahwa jarak dari pusat ke keliling lingkaran merupakan radius lingkaran. Radius merupakan jarak terpendek antara pusat lingkaran dan titik pada keliling.
Jarak terbesar pada lingkaran adalah panjang dari diameter lingkaran. Diameter merupakan jarak terpanjang antara dua titik pada keliling yang melewati pusat lingkaran. Karena diameter memotong lingkaran di titik terjauh dari pusat, jarak dari pusat ke titik tersebut akan mencapai nilai terbesar.
Sebagai contoh, jika Anda memiliki lingkaran dengan diameter 10 cm, maka jarak dari pusat ke keliling pada titik mana pun pada lingkaran akan selalu 5 cm, karena 5 cm merupakan panjang radius lingkaran.
Sifat Ketiga: Pengaruh Perubahan Jarak terhadap Keliling Lingkaran
Sifat ketiga dari jarak dari pusat ke keliling lingkaran adalah bahwa jika jaraknya berubah, keliling lingkaran juga akan berubah. Jarak yang lebih besar akan menghasilkan keliling yang lebih besar, sedangkan jarak yang lebih kecil akan menghasilkan keliling yang lebih kecil.
Untuk memahami sifat ini, kita perlu mengetahui hubungan antara jarak dari pusat ke keliling (radius) dengan keliling lingkaran. Rumus umum untuk menghitung keliling lingkaran adalah K = 2πr, di mana K merupakan keliling lingkaran dan r merupakan jarak dari pusat ke keliling (radius).
Jika jarak (radius) dari pusat ke keliling lingkaran diperbesar, maka keliling lingkaran juga akan menjadi lebih besar. Hal ini karena rumus keliling lingkaran memiliki faktor 2π yang dikalikan dengan jarak dari pusat ke keliling. Oleh karena itu, semakin besar nilai jarak tersebut, semakin besar pula nilai kelilingnya.
Sebaliknya, jika jarak (radius) dari pusat ke keliling lingkaran diperkecil, maka keliling lingkaran juga akan menjadi lebih kecil. Hal ini karena rumus keliling lingkaran memiliki faktor 2π yang dikalikan dengan jarak dari pusat ke keliling. Oleh karena itu, semakin kecil nilai jarak tersebut, semakin kecil pula nilai kelilingnya.
Jadi, sifat ketiga ini menunjukkan bahwa perubahan jarak dari pusat ke keliling lingkaran akan mempengaruhi nilai keliling lingkaran tersebut.







